ENCOUNTER with MATHEMATICS ----- 数学との遭遇

第１６回

Painleve 方程式 -- 新しい視点をめざして

２０００年６月３０日（金）(１４：３０～１８：１０) ～７月１日（土）(１０：３０～１６：５０)

於 : 東京都文京区春日１--１３--２７　中央大学理工学部

６月３０日(金)
１４：３０～１６：００ Painleve 方程式の数理 : 岡本和夫氏 (東大・数理)

１６：４０～１８：１０　Painleve 方程式は特殊関数を定義するか : 梅村浩氏 (名大・多元数理)

７月１日(土)
１０：３０～１１：３０有理曲面とPainleve 方程式の幾何 : 坂井秀隆氏 (東大・数理)

１１：５０～１２：５０有理曲面とPainleve 方程式の幾何 II : 坂井秀隆氏 (東大・数理)

１４：２０～１５：２０ Painleve 方程式の対称性 I : 山田泰彦氏 (神戸大・自然科学)

１５：５０～１６：５０ Painleve 方程式の対称性 II : 山田泰彦氏 (神戸大・自然科学)

別紙の趣旨に沿った集会の第16回を以上のような予定で開催いたします。非専門家向けに入門的な講演をお願い致しました。多く方々の御参加をお待ちしております。講演者による講演内容へのご案内を添付いたしますので御覧下さい。

連絡先 : 112-8551 東京都文京区春日 1-13-27 中央大学理工学部数学教室 tel : 03-3817-1745
ENCOUNTER with MATHEMATICS : e-mail : encmath@math.chuo-u.ac.jp
homepage : http://www.math.chuo-u.ac.jp/ENCwMATH
三松佳彦 : yoshi@math.chuo-u.ac.jp / 高倉樹 : takakura@math.chuo-u.ac.jp

Painleve 方程式

新しい視点をめざして

概要

Painleve 方程式の数理 : 岡本　和夫（東大・数理）

私は随分長い間，Painleve 方程式を研究対象としてきました。 Painleve 方程式というのは，19 世紀の終わり頃，微分方程式で定義される新しい特殊関数を探す，という問題意識のもとで，Painleve が発見した 6 つの 2 階非線形常微分方程式です。この問題意識は現在でも特別変わったものとは思っていませんが，古くさいと見られていたようで，しばらく放って置かれました。

私に求められている話は，Painleve 方程式の概略であろうと想像できますので，具体的な新しい話は他の講演者にお任せし，今考えている問題意識のようなものを併せて紹介しようと思っています。なお，最近「Painleve 方程式の数理」という題で話をする機会が多いのですが，内容は必ずしも同じではありません。今回は，Painleve 方程式の拡張について考えてみたいと思っています。

Painleve 方程式は特殊関数を定義するか : 梅村　浩（名大・多元数理）

Painleve 方程式に関する最も深刻な問は表題にした問である. すなわち,

問題. Painleve 方程式は本当に特殊関数を定義するのか.

Painleve 方程式は 100 年程前に発見された. 発見の原動力となったのは新しい特殊関数の追求である. 19 世紀の数学者には次のような問題意識があった. すなわち, 当時よく知られていた特殊関数である超幾何関数およびその合流, 楕円関数を一般化することによって, 新しい豊かな数学の世界が開けて来るのではないか. 一般化を考える上でモデルとなったのは Weierstrass の $\wp$ 関数であった. Painleve は動く特異点を持たない 2 階の代数微分方程式

$\begin{displaymath}y''= F(t,\, y, \, \, y') \leqno{(2)} \end{displaymath}$

を分類した. ここで, $F(t,\, y, \, y')$ は $t, \, y, \, y'$ の $\mathbb{C}$ -係数有理式である. その後, これらの代数微分方程式の表から知られた関数で積分できるものを消去した. その結果残ったのが、 6 つの Painleve 方程式である. ここから自然に, 上に述べた疑問が生じるのである.

これまでに挙がった Painleve 方程式研究の成果は次のようである.

(i): Painleve 方程式はモノドロミー保存変形を記述する. この形で Painleve 方程式は数理物理学に出現した(R. Fuchs, Garnier, 佐藤学派).
(ii): Backlund 変換および Hamilton 構造の発見(岡本和夫).
(iii): $\tau$ 関数の理論(佐藤学派, 岡本).
(iv): 初期値空間の幾何学的研究(岡本).
(v): Painleve 方程式の還元不能性の証明. Painleve 方程式の古典解の決定(西岡, 岡本, 野海, 村田, 渡辺等) .
(vi): Painleve 方程式が生成する特殊多項式の研究(Yablonskii, 岡本, 野海, 岡田、種子田)

これらの成果ははたして Painleve 方程式が特殊関数を定義することを意味するのであろうか.

有理曲面とPainleve 方程式の幾何 : 坂井　秀隆（東大・数理）

曲面を与えるということは、何枚かの座標系を用意しておいてそれらを張り合わせるということである。もう少し詳しく言うと、座標を張り合わせるという言うことは、それらの間の座標変換を与えることである。

簡単な曲面を作って張り合わせの変換で遊んでいると、自然に曲面の対称性が見えて来る。これらの変換は幾何学的によく分かる形で定式化できる。 Picard 群という格子の自己同型群で、行列でかける。

本当に簡単な場合にはこの対称性は有限群でかけてしまう。もう少し頑張って、例えば射影平面の 9 点 blow-up 等を考えると無限群が出て来る。この場合この対称性には ${\mathbb Z}$ が部分群として含まれていて、その作用を順々に見ていくことで、離散的な時間発展つまり差分方程式と思うことができる。

曲面を退化させることで、このそれぞれのステップを無限小に持っていくと微分方程式がでてきた。 Painleve 方程式だ。

Painleve 方程式の対称性 : 山田　泰彦（神戸大・自然科学）

本講演では, この数年間の野海正俊氏(神戸大)との共同研究の内容について述べたいと思います. 対称性を基本にしてPainleve 方程式を眺める, というのが研究の主題です.

Painleve 方程式のような微分方程式に対して, その対称性とは解空間の対称性のことと考えてください. あるいは, 解を解にうつす変換群の研究と言ってもよいでしょう. 我々はこのような変換を Bäcklund 変換と呼びます.

例として取り上げますのは, Painleve 方程式のうちの第4番 P_IVで, 我々はこれを次のように表します,

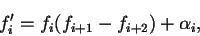$\begin{displaymath}f_i'=f_i(f_{i+1}-f_{i+2})+\alpha_i, \end{displaymath}$

(1)

ここで '=d/dx は独立変数 x についての微分, $\alpha_i$ は $\alpha_0+\alpha_1+\alpha_2=1$ を満たすパラメータ, f_i=f_i(x) は f₀+f₁+f₂=x を満たす未知関数です. この例では, 添字はいつも ${\bf Z}/3 {\bf Z}$ の元と見てください.

この形式における Bäcklund 変換変換 s₀, s₁, s₂, $\pi$ は次であたえられます.

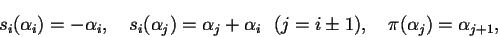$\begin{displaymath}s_i(\alpha_i)=-\alpha_i, \quad s_i(\alpha_j)=\alpha_j+\alpha_i \ \ (j=i\pm 1), \quad \pi(\alpha_j)=\alpha_{j+1}, \end{displaymath}$

(2)

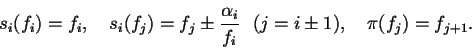$\begin{displaymath}s_i(f_i)=f_i, \quad s_i(f_j)=f_j\pm \frac{\alpha_i}{f_i} \ \ (j=i\pm 1), \quad \pi(f_j)=f_{j+1}. \end{displaymath}$

(3)

これらの変換は微分方程式を不変に保ち, 次の関係式を満たします,

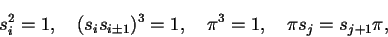$\begin{displaymath}s_i^2=1, \quad (s_is_{i \pm 1})^3=1, \quad \pi^3=1, \quad \pi s_j=s_{j+1} \pi, \end{displaymath}$

(4)

すなわち, A⁽¹⁾₂ 型アフィンワイル群(の拡張)を生成します.

このような話は, 記述の仕方は異なりますが, 80年代の岡本さんの研究などにより知られていたことです. 我々は, このような話の他のルート系への拡張を考えます.

Last Modified : Jun 03, 2000 : 15:55