非線型の特殊函数論 --- Painleve 方程式の応用
概要
非線型の特殊函数論〜Painlevé方程式の応用
大山 陽介 (阪大・情報)
初等函数を超えた特殊函数の研究は、1694年に Johann Bernoullis が
Riccati 方程式
![]() を調べたことに始まる。この方程式は(今で言う)
Bessel
函数
を調べたことに始まる。この方程式は(今で言う)
Bessel
函数
![]() を用いて解くことができるが、微分方程式を求積すること
を
目標とした当時においては、べき級数によってようやく解かれたこの方程式は
斬新なものであったと
思われる。
を用いて解くことができるが、微分方程式を求積すること
を
目標とした当時においては、べき級数によってようやく解かれたこの方程式は
斬新なものであったと
思われる。
その後、さまざまな「特殊函数」が個別に研究されてきた。「特殊函数」の定 義を述べることは難しいが、 その特徴としては
- 数理科学に幅広い応用をもつ
- 計算可能である
特殊函数の組織的研究は Whittaker-Watson にまとめられた。「特殊函数」を 書名に冠した最初の本と思われる Magnus-Oberhettinger が出版された1943年頃には `Modern Analysis' の題 名 が時代にあわなくなって きたことは確かである。また、「特殊函数」自体が関数解析の 発展などの陰で、多くの数学者から古臭い数学と思われたことも確かであろう。 しかしながら、 近年、再び特殊函数の研究が Modern Analysis の中心として復活してきたこ とは疑う余地もない。 青本・Gelfand らによる多変数の超幾何関数が組織的な研究、量子群の発展に ともなう q-analogue analysis、そして、非線型の特殊函数にあたる Painlevé 方程式の研究など が1980年代以降爆発的に 進んできた。
Whittaker-Watson の時代、すでにこれらの研究は萌芽としてあったが、どれ もあらわには 取り上げられていない。初版(Watson は2版以降共著)が出た1902年は、まさ に Painlevé方程式が 生れつつあった時期であり、教科書としてまとめるには時期尚早であったため である。
ENCOUNTER with MATHEMATICS 第34回では、特殊函数の復権という動きの中で、 非線型の特殊函数として Painlevé方程式をとりあげる。 第16回(2000年)にも「Painlevé 方程式 - 新しい視点をめざして」で取り上げられたテーマであり、そこでも梅村浩 氏 (名大・多元数理) が「Painlevé 方程式は特殊関数を定義するか」と題してこの問題を扱って いるが、5年たった今では Painlevé 方程式は特殊函数として確固とした位置を数学の中に占めている と確信する。
かつて H. Poincaré が "Les mathématiques constituent un
continent
solidement agencé, dont tous les pays sont bien reliés les
uns aux
autres; l'oeuvre de Paul Painlevé est une île originale et
splendide
dans l'océan voisin." と評したが、
現代の Painlevé 方程式の研究は数学の世界の絶海の孤島ではなく、代数幾
何、表現論、値分布論などの
伝統的な数学と密接な関係を持ちつつ、微分幾何、位相的場の理論、散乱理論、
など様々な応用が
研究されつつある。今回は、Painlevé 方程式の入門的な話(大山)から初
めて、ソリトン方程式との
関連(筧)、ランダム行列への応用(村瀬)など、「非線型の特殊函数」とし
ての Painlevé 方程式と
その応用について解説したい。
以下の web site (阪大・大山氏)で
パリ5区にある Square Paul-Painleve の写真を
ご覧いただけます。
http://www.math.sci.osaka-u.ac.jp/~ohyama/frame/newton/square.html
1.変形理論からみた Riemann-Hilbert 問題〜
Painlevé 方程式入門
2.モノドロミ可解な Painlevé 函数
大山 陽介(阪大・情報)
「与えられたモノドロミを持つ方程式は存在するか」という Riemann-Hilbert 問題は、数学の様々な 分野で形を変えて表れる基本的な問題である。Riemann-Hilbert 問題は、その 当初から変形理論と密接な 関係をもって研究されてきた。数学の対象はパラメタを含んだ形で定式化する ほうが見通しがよく、さらに そのパラメタに関する無限小変形を考えることで新しい世界が開けるのである。 そこで前半では、 Riemann-Hilbert 問題を変形理論を使って解くという Schlesinger 以来の古 くて新しい話をキーにしながら、 Painlevé 方程式自体の入門を与えることを目標にする。
逆に、Painlevé 方程式の側から Riemann-Hilbert 問題を見た場合、モノド ロミ保存変形と 言いつつも、不変量であるモノドロミ自体にはいっさい情報がないように見え るのが不満である。 一般に、ホモロジー・ホモトピーなどの「不変量」も、具体的に計算するのは 実は大変だったりする。 本来、Painlevé 函数そのものがモノドロミ・データを所有しているはずで あり、後半では、 問題を逆にして「モノドロミが計算可能な」Painlevé 函数について話をす る。 なお、ここでも「計算可能」意味が曖昧のままである。
J. Bernoullis が Riccati 方程式に立ち向かった17世紀以来、「計算可能」
の定義をすることが
特殊函数のテーマの一つであった。「可積分系とは何か」という問題とも共通
する問題であり、さらには
「微分方程式を解くとはどういうことか」という根源的な問題にもつながって
いく。しかし、この300年間で
「計算可能」の定義づけに特殊な場合に限っても成功したのは、Liouville、
Picard-Vessoit、梅村など
少数しかいない。他に、H. A. Schwarz による超幾何函数の代数解の分類(さ
らに C. Jordan の研究が続く)も、
超幾何方程式の積分可能性の問題と考えることができる。「モノドロミ可解」
の定義づけはまだ遠い先に
あるが、こうした問題と深くかかわっている。
1.ガウスを超えてパンルヴェへ:
新しい確率分布函数の話
2.特殊函数としての生成函数:幾何を足す
村瀬 元彦(UC Davis)
サイコロを何回も振れば、だいたい6回に1度は1 の目が出る。 さらに精密に、実際に1の目が出た回数と期待値と の差をサイコロを 振った回数の平方根で割った量は、ガウス分布に従 う(大数の法則)。
過去10年ほどの間に数学の様々な分野で、ガウス 分布には従わない もののきわめて広汎に現れる普遍的な確率分布が存 在することが発見 された。例えば、マスメの数を無限大にとばしたと き、最も典型的な ヤング図形がどんな形になるかは簡単に求められる が、実際の形と その期待値からのずれはガウス分布には従わない。
もっと簡単な例として、百科事典をでたらめに並べ たとき、もとの 順序になっている巻が何巻あるかを問題にしよう。 全巻を正しい順序に 戻すには、元々正しい順序のものはそのままにし て、正しくないもの だけを並べ替えればよい。だからこの数には意味が ある。この数の 分布が決定されたのはやっと1999年のことであ る。
不思議なことに、これらの分布はエルミート行列を でたらめに与えた ときその最大固有値がどのように分布するかを調べ て得られた トレーシー・ウィダムの法則に従う。トレーシー・ ウィダム分布とは、 ガウス分布に現れる指数関数を第2パンルヴェ超越 函数で置き換えた ものである。
正しい順序にある百科事典の巻数とエルミート行列 の固有値とが 同じ分布を示すのにはもちろんわけがある。実に、 グロモフ−ウイッテン 理論、ウイッテン−コンツェヴィッチ理論、佐藤の KP理論等がその背景に あるのだ。
この不思議なつながりを2回に分けてお話ししたい。
ソリトンから見たパンルヴェ方程式
筧 三郎(立教大・理)
パンルヴェ方程式は,様々な形で数理物理の研究に現れる。 本講演では,その中でも特に,ソリトン方程式の 相似簡約 (Similarity Reduction) という話題に注目する。 ここで「相似簡約」とは,自己相似解 (方程式を変えないスケール変換に関して不変な解)を 考えることで偏微分方程式を常微分方程式に対応付けることであり, 偏微分方程式を研究する一つの手法として古くから用いられてきた。
AblowitzとSegurは,1977年の論文で,I型からIII型のパンルヴェ方程式が,
ソリトン方程式からの相似簡約として得られることを示した
[1]。
例えば,![]() が変形Korteweg-de Vries (mKdV) 方程式
が変形Korteweg-de Vries (mKdV) 方程式
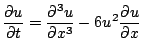 |
を満たすとき,
により1変数の問題に帰着され,パンルヴェII型方程式が導かれる。
一方,ソリトン方程式を扱う場合における最も普遍的な視点の一つとして, いわゆる「KP階層」の理論がある[2, 3]。 その立場から眺めると, 全ての型のパンルヴェ方程式は,KP階層(あるいは戸田階層)の 相似簡約としてとらえることができる。
講演では,それぞれの型のパンルヴェ方程式がKP階層にどのように
埋め込まれているかを解説し,そこから得られる諸分野
(物理系の相関関数,曲面論,関数論,表現論等)への応用について紹介する。
参考文献
[1]
M.J. Ablowitz and H. Segur,
Exact linearization of a Painlevé transcendent,
Phys. Rev. Lett. 38 (1977), 1103-1106.
[2]
佐藤幹夫 述,野海正俊 記 「ソリトン方程式と普遍グラスマン多様体」,
上智大学数学講究録 no.18,1984年6月.
[3]
高崎金久 著,
「可積分系の世界 −戸田格子とその仲間−」,共立出版,2001年3月.